Trinásť detí sedí okolo okrúhleho stola. Chlapci sa rozhodnú, že budú stále klamať dievčatám a hovoriť pravdu chlapcom. Dievčatá sa rozhodnú, že budú stále klamať chlapcom a hovoriť pravdu dievčatám. Jedno z detí povie svojmu susedovi vpravo: „Väčšina z nás sú chlapci.“ Potom tento sused povie svojmu susedovi vpravo: „Väčšina z nás sú dievčatá.“ A takto sa budú výroky striedať ďalej, až kým posledné dieťa povie prvému: „Väčšina z nás sú chlapci.“ Koľko chlapcov je pri stole?

Rýchlik mal $2476$ vagónov, ktoré boli buď žlté, alebo čierne. Prvý vagón bol žltý. Deti si hneď všimli, že ak je nejaký vagón žltý, tak vagón $5$ a $13$ miest pred ním je žltý a aj vagón $5$ a $13$ miest za ním je žltý. Koľko čiernych vagónov mal vlak?

Každý z $1000$ kompótov má na sebe iné prirodzené číslo od $1$ do $1000$. Jožo má k dispozícii $10$ poličiek, na ktoré chce kompóty uložiť. Ako to má urobiť, aby pre všetky dvojice kompótov na jednej poličke platilo, že kompót s ich rozdielom sa na tej poličke nenachádza.
BONUS (za sladkú odmenu): Vie to Jožko zvládnuť aj s menším počtom poličiek? Ak áno, tak s akým a ako?

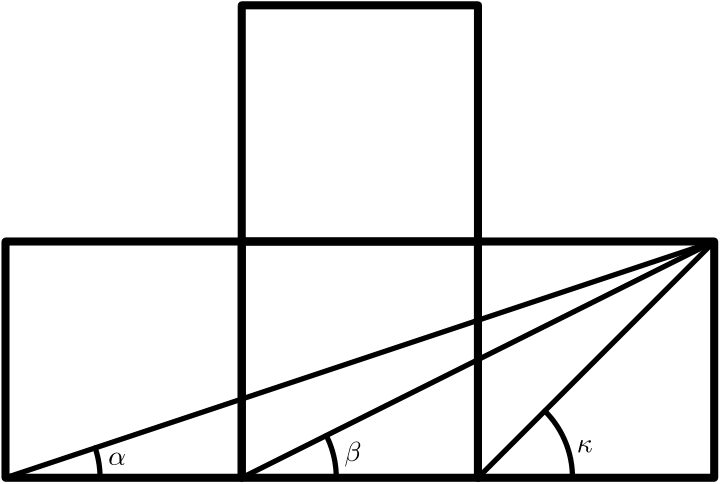
Obrázok je zložený zo $4$ zhodných štvorcov. Dokážte, že súčet veľkostí uhlov $\alpha$ a $\beta$ je rovný veľkosti uhla $\kappa$.

Predavač im povedal, že každé z použitých písmen predstavuje inú cifru (napríklad $K$ by mohla byť $0$). Tiež im povedal, že ceny troch jeho produktov, konkrétne $\overline{ABACDE}$, $\overline{CAFDG}$ a $\overline{CHHBAED}$, predstavujú dĺžky strán nejakého trojuholníka (môže existovať trojuholník, ktorého strany majú tieto dĺžky), pričom $A$ a $C$ sú rôzne od $0$. Aké sú ceny týchto troch produktov?

S gejmbojom sa nedá prehrať práve vtedy, ak je tvar jeho displeja zložený z dvoch prelínajúcich sa rovnobežníkov $ABCD$ a $AEFG$, pričom platí, že bod $E$ je ľubovoľne umiestnený na strane $BC$ a bod $D$ je ľubovoľne umiestnený na strane $GF$. Aký je pomer obsahov týchto rovnobežníkov?

Vyšetrovatelia si vypočuli štyri deti. Polícia od svedkov vedela, že každé z detí bolo pri stole s gejmbojom práve raz. Pred výsluchom sa však deti dohodli, že vyšetrovateľom budú stále klamať. Každý uviedol dve výpovede:

• Svorad: „Nikto z nás štyroch gejmboj nevymenil. Keď som odišiel, lebo mi bolo treba na záchod, gejmboj bol ešte pravý.“
• Andrej: „Ja som ku stolu prišiel ako druhý. Keď som prišiel, gejmboj bol už vymenený.“
• Marienka: „Ja som ku stolu prišla ako tretia. Keď som prišla, gejmboj ešte nebol vymenený.“
• Jozefína: „Ten, kto gejmboj vymenil, neprišiel po mne. Keď som prišla, gejmboj už bol vymenený.“

Tabuľka $3\times3$ štvorcov je vyplnená číslami od $1$ do $9$, každým práve raz. V strede každého štvorca $2\times2$ je kruh a v ňom je napísaný aritmetický priemer čísel v štvorci. Ako treba rozostaviť čísla do tabuľky, aby bol aritmetický priemer čísel z kruhov najväčší možný?

Vypočítajte veľkosť uhla $BAC$ v trojuholníku $ABC$, keď viete, že je trikrát menší ako uhol $BOC$, pričom $O$ je stred kružnice vpísanej trojuholníku $ABC$ (Kružnica vpísaná trojuholníku je taká kružnica, ktorá sa dotýka všetkých strán trojuholníka. Jej stred leží na priesečníku osí uhlov trojuholníka).

Na ruletovom stole je štvorcová sieť o rozmeroch $4\times4$. Cieľom hry je zistiť, koľko navzájom nezhodných úsečiek (úsečiek s rôznymi dĺžkami) s krajnými bodmi v mrežových bodoch štvorcovej siete existuje v tejto sieti. Koľko ich existuje, ak by sieť mala rozmery $10\times10$?

Kartón v tvare štvorca $ABCD$ má stranu dlhú $36$. Bod $E$ leží na strane $AB$ tak, že $|EB| = 12$, bod $F$ leží v strede strany $BC$ a bod $G$ na strane $CD$ tak, že $|CG| = 12$. Aký je obsah plochy ležiacej v trojuholníku $EFG$, ale mimo trojuholníka $AFD$?

Bezdomovec im dal za úlohu dokázať, že ak $n$ je celé číslo väčšie ako $6$, a ak $n-1$ a $n+1$ sú prvočísla, tak číslo $n\cdot n(n\cdot n + 16)$ je deliteľné číslom $720$.
Nejaké čiastkové body sa budú dať získať aj za dokázanie deliteľnosti menšími číslami. Preto neváhajte a pošlite aj nekompletné riešenia ;-).